Desenho de objetos em OpenGL -- Computação Gráfica

jSSeção 4.3  

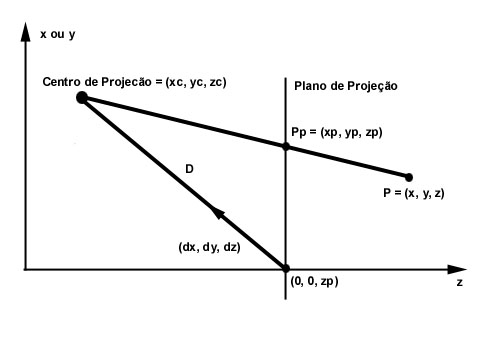
Para simplificar a compreensão dos parâmetros dessa matriz genérica, utilizaremos a figura 4.3.1, que mostra a projeção do ponto P sobre o plano de projeção (ponto Pp). Vamos assumir que o plano de projeção é o plano z = zp.

Figura 4.3.1 - O ponto Pp é projeção do ponto P sobre o plano de projeção.

O plano de projeção é perpendicular ao eixo z na distância zp da origem. Observe que o ponto (0, 0, zp) é ponto de interseção do plano de projeção com o eixo z. Logo zp é a posição do plano de projeção em relação ao eixo z, que como foi dito anteriormente, é um dado necessário para se definir a representação matemática de uma projeção. 

O centro de projeção está a uma distância D do ponto (0, 0, zp), a importância de se conhecer a posição do centro de projeção para a representação matemática, está no fato desta posição ser usada para se calcular o valor de D que é usado na matriz genérica.

A direção de (0, 0, zp) para o centro de projeção é dada pela direção do vetor normalizado (dx, dy, dz). A direção de (dx, dy, dz) é chamada de direção de projeção. 

Resumindo, para construirmos uma matriz, a qual chamaremos de Mgeral, que represente qualquer projeção, será necessário sabermos apenas os valores de zp, (dx, dy, dz) e D.

Com todos os parâmetros especificados, podemos agora definir a matriz genérica de projeção (figura 4.3.2), não entraremos em detalhes sobre a descrição matemática da qual essa matriz resulta, mas esta pode ser obtida na bibliografia complementar:

A partir dessa matriz geral é possível se definir qualquer tipo de projeção. Deve-se apenas respeitar as características gerais de projeções paralelas e perspectivas, além de características específicas de casos especiais dessas projeções.

Veja um exemplo do uso de uma matriz de projeção, por enquanto não se preocupe com os valores da matriz utilizados no exemplo. Em OpenGl para especificar sua própria matriz de projeção é necessário declarar uma matriz de 16 elementos (4 X 4) conforme abaixo:

    >> GLfloat mprojecao [16];  // declaração de uma matriz 4x4

O formato para esta matriz é descrito abaixo:

Figura 4.3.3 - Formato de uma matriz em OpenGl.

Para se inserir os valores na matriz deve-se utilizar o seguinte comando de atribuição:

mprojecao[ posição ] = valor a ser inserido;

Para se inserir, por exemplo, os valores correspondentes a primeira coluna da matriz (valores que são constantes), temos:

    >> mprojecao[0] = 1;   // inserindo 1 em A0

    >> mprojecao[1] = 0;   // inserindo 0 em A1

    >> mprojecao[2] = 0;   // inserindo 0 em A2

    >> mprojecao[3] = 0;   // inserindo 0 em A3

De forma semelhante se deve fazer para se inserir valores nas outras posições da matriz. Depois de todos os valores inseridos na matriz, ela já está pronta para ser utilizada. Para se carregar esta matriz deve-se utilizar o método descrito abaixo: 

glLoadMatriz( matriz );

Veja no código abaixo um exemplo de como utilizar esta matriz de projeção em OpenGl:

      >>  glLoadMatriz (mprojecao);   // carregando a matriz mprojecao
     

[principal]

[anterior]

[próxima]