Bactracking

Definição:

É uma estratégia de busca de alternativas possíveis para uma solução, semelhante à uma busca em profundidade. Essa estatégia consiste em prever a existencia de soluções não analisadas no processo de busca da solução. Quando se detecta a impossibilidade de se encontrar uma solução via uma determinada forma, possibilidades anteriores que já haviam sido resolvidas são revistas em favor das possibilidades que ainda não tinham sido analisadas.

Exemplo:

Suponha o seguinte problema:

Queremos colorir os vértices de um grafo não direcional com 3 cores de maneira que cada vértice tenha um cor diferente da cor de seus vizinhos.

Dado um grafo, pode não haver solução para o problema, pode haver uma ou pode haver várias soluções.

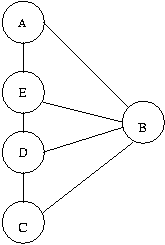
Considere que vamos resolver o problema para o grafo abaixo:

Tentando resolver o problema, poderiamos colocar a cor 1 no vértice A, a cor 2 no vértice B, a cor 1 no vértice C, a cor 3 no vértice D e então não haveria nenhuma cor possível para colocar no vértice E. Neste ponto então voltamos ao vértice D (mas a única possível para D seria 3 mesmo) e então, voltamos do vértice D ao vértice C, onde poderíamos ter escolhido a cor 3. Alteramos então nossa solução de cor para o vértice C que passa a ter cor 3. Neste ponto, a cor do vértice D ainda não havia sido escolhida, então vamos continuar a solucionar o problema a partir daqui. Teremos então que escolher a cor 1 para o vértice D e a cor 3 para o vértice E.

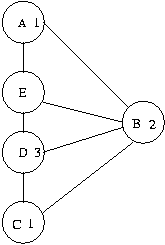
Essa volta à solução de um problema parcial (escolha da cor do vértice C) é chamada de backtrack.

Se depois dessa solução quisermos encontrar outras soluções para o problema, ainda podemos testar outras possibilidades de cores para alguns vértices que ainda não tinham sido analisadas. Caso não existam mais soluções, todas as possibilidades terão sido analisadas antes que se tenha certeza de que não existe outra solução.